Lab 2 - The Collatz Conjecture

The Collatz Conjecture

The Collatz Conjecture is a famous unproven conjecture in mathematics.

Problem Statement

Consider the following operations on any positive integer:

• If the number is even, divide it by two
• If the number is odd, multiply it by three and add one

Repeat these steps by taking the output as the new input

The conjecture states that no matter what integer you choose as your starting value, you will end up at 1.

Okay. So What?

It currently has not been proven whether this is true or false.

It seems like an extremely easy problem to get a handle on, and yet expert mathematicians are unable to determine whether it is true for every number or whether there are some exceptions.

For more, you can check out this nice pop-sci write-up in Quanta Magazine. But we aren’t really interested in solving it; we just want to implement it.

Lab Overview

Each of you will make your own script for the collatz conjecture which takes a number, performs the operations above, and outputs the chain of numbers taken to get to the answer.

You will build up this program with additional functionality over the course of the lab today.

Assessment

For Proficiency credit, turn in Part 1.

For Mastery credit, turn in Parts 1 and 2.

A Note on Learning

Some of the things you will be doing in lab today are not things I’ve taught you explicitly. That is, you have all the tools to do the tasks required — variables, if statements, while loops, and for loops — but some of the things you do will do to combine those pieces aren’t things I’ve demonstrated. This is intentional; struggling with a new concept and trying your own approach, while frustrating, is an important part of deeply learning.

Here’s some steps to working on something you feel stumped on:

1. Just try something! The nice thing about programming is you can always run the program to see if what you tried worked. If it didn’t, that’s okay; you can try again.
2. Ask your peers at your table. If they are also stumped, you are probably stumped in different ways, and you can work together to approach the problem from a new angle.
3. Call me over to ask for help. Spoiler: I probably won’t just give you the answer, but I’ll direct you towards some ideas to try out.

Part 1: Basic Collatz Conjecture

First, create a file called collatz1.py in which to do your lab.

1a: Initial Program

Write a program that takes a number from the user and outputs the series of numbers leading to 1 when following the steps of the collatz conjecture. It should also output whether the number was multiplied or divided. Here is a sample output:

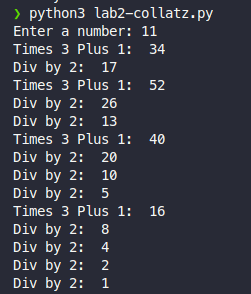
You can customize the actual output however you like.

Make sure that you print the final number (1).

Bonus: The numbers you have are probably printing out as floats, e.g. 1.0 rather than 1. How could you turn them back to ints?

1b: Length of the Chain

Now that you have a basic implementation of the collatz conjecture, maybe we want to know how long it took us to get to the end of the chain.

Modify your code to output the length of the path to get to 1. Don’t include the initial number in the chain length (e.g., the input 2 should give a chain length of 1).

Here’s some sample output:

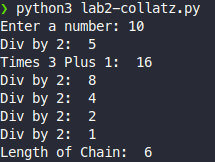
Save this file as collatz1.py.

Part 2: The Longest Chain

Create a new file called collatz2.py in which to do the second half of the lab. You can reuse any of the code from collatz1.py that you want.

2a: Set Range

Now, maybe we’re interested in finding out not what the chain is, but what the longest chain within a particular range is.

For example, the longest chain between the numbers 2 to 5 is at the number 3.

2 > 1: Length 1
3 > 10 > 5 > 16 > 8 > 4 > 2 > 1: Length 7
4 > 2 > 1: Length 1
5 > 16 > 8 > 4 > 2 > 1: Length 5

Your job is to have your program find what number between 2 and 1000 has the longest chain. You should output both what the number is and the length of the chain. You should NOT output the chain itself.

Here is an example output for the numbers between 2 and 10.

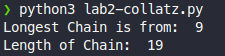
2b: User-Defined Range

In one more modification to this program, allow your user to pick the range to output. They should be asked to enter two numbers, a start and a stop. Your program should find the longest chain between the start and stop, including the number indicated for the stop. It should also tell them the length of the chain, as before.

Here is an example output:

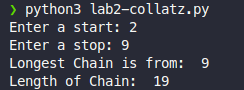
Save this file as collatz2.py. Submit both your files to Canvas as your lab.